Decoding coefficients recovery based on modified gauss-jordan elimination for tampered content reconstruction

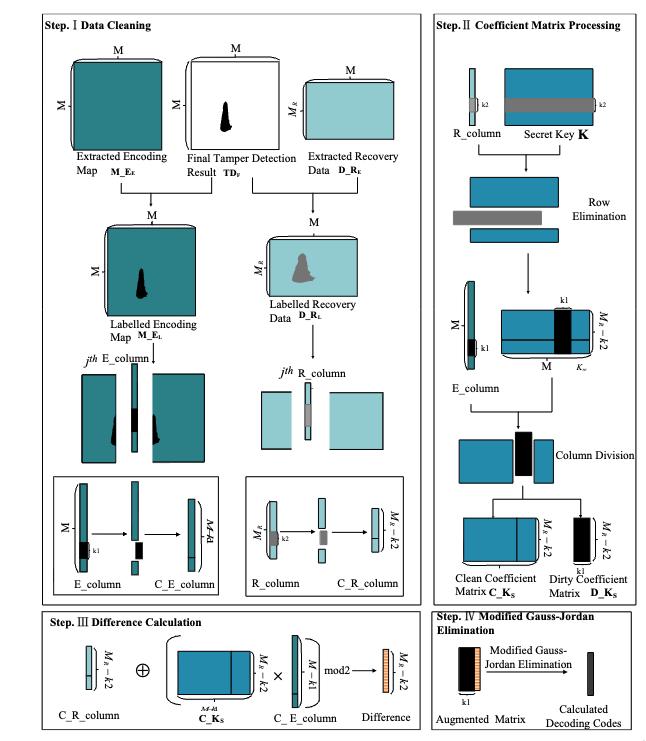
The widespread availability of image editing applications has increased the risk of digital image tampering. Although existing studies can accurately localize tampered regions, they still face limitations in recovering images with high quality, especially under extensive tampering. This limitation mainly arises from the loss of recovery data when large areas are manipulated. To address this issue, we propose a mathematical watermarking scheme for detecting and recovering tampered regions. Our approach employs the Set Partitioning In Hierarchical Trees (SPIHT) algorithm to encode images, thereby generating encoded coefficients that serve as recovery data. However, when extensive tampering leads to substantial loss of these recovery data, conventional decoding becomes ineffective. To overcome this, we propose a modified mechanism based on Gauss-Jordan elimination to effectively retrieve missing data. Furthermore, to improve recovery performance, the recovery process is divided into two phases: coefficient recovery and image recovery. During the coefficient recovery phase, a Modified Gauss-Jordan Elimination-based Decoding Coefficient Recovery method is employed to calculate the missing recovery coefficients. Subsequently, these recovered coefficients are employed in the image recovery phase to reconstruct the original image. Comparative experiments show that the proposed method achieves superior recovery performance, with an average PSNR improvement of about 2 dB under different tampering rates. Even when the tampering rate reaches up to 90%, the image can still be recovered. These results demonstrate the strong recovery capability of the proposed method under extensive tampering.